本文由 简悦 SimpRead 转码， 原文地址 blog.csdn.net

我们首先来看一下什么是前向星.

前向星是一种特殊的边集数组, 我们把边集数组中的每一条边按照起点从小到大排序, 如果起点相同就按照终点从小到大排序,

并记录下以某个点为起点的所有边在数组中的起始位置和存储长度, 那么前向星就构造好了.

用 len[i] 来记录所有以 i 为起点的边在数组中的存储长度.

用 head[i] 记录以 i 为边集在数组中的第一个存储位置.

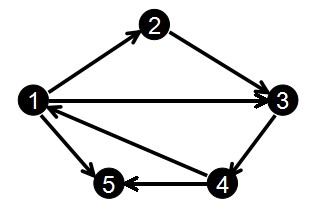
那么对于下图:

**
**

我们输入边的顺序为:

1 2

2 3

3 4

1 3

4 1

1 5

4 5

那么排完序后就得到:

编号:     1      2      3      4      5      6      7

起点 u:    1      1      1      2      3      4      4

终点 v:    2      3      5      3      4      1      5

得到:

head[1] = 1    len[1] = 3

head[2] = 4    len[2] = 1

head[3] = 5    len[3] = 1

head[4] = 6    len[4] = 2

但是利用前向星会有排序操作, 如果用快排时间至少为 O(nlog(n))

如果用链式前向星, 就可以避免排序.

我们建立边结构体为:

struct Edge

{

int next;

int to;

int w;

};

其中 edge[i].to 表示第 i 条边的终点, edge[i].next 表示与第 i 条边同起点的下一条边的存储位置, edge[i].w 为边权值.

另外还有一个数组 head[], 它是用来表示以 i 为起点的第一条边存储的位置, 实际上你会发现这里的第一条边存储的位置其实

在以 i 为起点的所有边的最后输入的那个编号.

head[] 数组一般初始化为 - 1, 对于加边的 add 函数是这样的:

1
2
3
4
5
6
7
void add(int u,int v,int w)
{
    edge[cnt].w = w;
    edge[cnt].to = v;
    edge[cnt].next = head[u];
    head[u] = cnt++;
}

初始化 cnt = 0, 这样, 现在我们还是按照上面的图和输入来模拟一下:

edge[0].to = 2;     edge[0].next = -1;      head[1] = 0;

edge[1].to = 3;     edge[1].next = -1;      head[2] = 1;

edge[2].to = 4;     edge[2],next = -1;      head[3] = 2;

edge[3].to = 3;     edge[3].next = 0;       head[1] = 3;

edge[4].to = 1;     edge[4].next = -1;      head[4] = 4;

edge[5].to = 5;     edge[5].next = 3;       head[1] = 5;

edge[6].to = 5;     edge[6].next = 4;       head[4] = 6;

很明显, head[i] 保存的是以 i 为起点的所有边中编号最大的那个, 而把这个当作顶点 i 的第一条起始边的位置.

这样在遍历时是倒着遍历的, 也就是说与输入顺序是相反的, 不过这样不影响结果的正确性.

比如以上图为例, 以节点 1 为起点的边有 3 条, 它们的编号分别是 0,3,5   而 head[1] = 5

我们在遍历以 u 节点为起始位置的所有边的时候是这样的:

for(int i=head[u];~i;i=edge[i].next)

那么就是说先遍历编号为 5 的边, 也就是 head[1], 然后就是 edge[5].next, 也就是编号 3 的边, 然后继续 edge[3].next, 也

就是编号 0 的边, 可以看出是逆序的.